Две прямые AB и CD называются параллельными , если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать (AB|| CD). Угол между параллельными прямыми равен нулю.
Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми,- расстояние между ними.
Аксиома: через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Свойства параллельных прямых:
1. Если две прямые параллельны третьей прямой, то они параллельны между собой.
2. Если две прямые перпендикулярны третьей прямой, то они параллельны друг другу.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов (рис.13), которые попарно называются:

1) соответственные углы (1 и 5; 2 и 6; 3 и 7; 4 и 8 );
углы попарно равны : (https://pandia.ru/text/78/187/images/image003_66.gif" width="11" height="10 src=">5; https://pandia.ru/text/78/187/images/image003_66.gif" width="11" height="10">6; https://pandia.ru/text/78/187/images/image003_66.gif" width="11" height="10">7; https://pandia.ru/text/78/187/images/image003_66.gif" width="11" height="10">8 );
2) внутренние накрест лежащие углы (4 и 5; 3 и 6 ); они попарно равны ;
3) внешние накрест лежащие углы (1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы (3 и 5; 4 и 6 ); сумма односторонних углов равна 180 °
(https://pandia.ru/text/78/187/images/image003_66.gif" width="11" height="10">5 = 180° ; 4 + 6 = 180°);
5) внешние односторонние углы (1 и 7; 2 и 8 ); их сумма равна 180° (https://pandia.ru/text/78/187/images/image003_66.gif" width="11" height="10">7 = 180°; 2 + 8 = 180°).
Теорема Фалеса. При пересечении сторон угла параллельными прямыми (рис.16) стороны угла делятся на пропорциональные отрезки:
Подобные треугольники.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Сходственные стороны подобных треугольников - это стороны, лежащие напротив равных углов.
https://pandia.ru/text/78/187/images/image006_51.gif" alt="подобные треугольники" width="13" height="14">A
= https://pandia.ru/text/78/187/images/image006_51.gif" alt="подобные треугольники" width="13" height="14">B = B1, С = С1
и ![]() Число k
, равное отношению сходственных сторон треугольника называется коэффициентом подобия
.
Число k
, равное отношению сходственных сторон треугольника называется коэффициентом подобия
.
Признаки подобия:
1. Если два угла одного треугольника соответственно равны двум углам другого, то треуг-ки подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами , равны , то треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого , то такие треугольники подобны.
Следствия: 1. Площади подобных треугольников относятся как квадрат коэффициента подобия:
2. Отношение периметров подобных треугольников и биссектрис , медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Параллельные прямые
. Расстояние между
параллельными прямыми
.
.
Соответственные углы
.
Внутренние и внешние накрест
лежащие углы
.
Внутренние и внешние односторонние углы .
Углы с соответственно
перпендикулярными сторонами
.
Пропорциональные отрезки
.
Теорема Фалеса.
Две прямые AB и CD ( рис.11 ) называются параллельными , если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Обозначение: AB || CD . Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой. Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Угол между двумя параллельными лучами равен нулю, если у них одинаковые направления, и 180 ° , если их направления противоположны. Все перпендикуляры ( AB , CD , EF , рис.12) к одной и той же прямой KM параллельны между собой. Обратно, прямая KM , перпендикулярная к одной из параллельных прямых, перпендикулярна и к остальным. Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми, есть расстояние между ними.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов (рис.13), которые попарно называются:
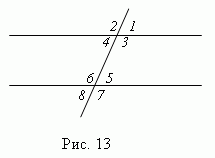
1) соответственные углы (1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно
равны: ( 1 = 5; 2 = 6; 3 = 7; 4 = 8 );
2) внутренние накрест лежащие углы (4 и 5; 3 и 6 ); они попарно равны;
3) внешние накрест лежащие углы (1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы (3 и 5; 4 и 6 ); их сумма равна 180 °
( 3 + 5 = 180
° ; 4 + 6 = 180 ° );5) внешние односторонние углы (1 и 7; 2 и 8 ); их сумма равна 180 °
( 1 + 7 = 180 ° ; 2 + 8 = 180 ° ).
Углы с соответственно параллельными сторонами либо равны друг другу ( если они оба острые, или оба тупые, 1 = 2 , рис.14), либо их сумма равна 180 ° ( 3 + 4 = 180 ° , рис.15).
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Угол между прямыми
Цели и задачи урока: Сформировать понятие угла между: Пересекающимися; Параллельными; скрещивающимися прямыми. Научиться находить угол между: Пересекающимися; параллельными; скрещивающимися прямыми.
Вспомним: Основание призмы ABCDA 1 B 1 C 1 D 1 – трапеция. Какие из следующих пар прямых являются скрещивающими?
Расположение прямых в пространстве и угол между ними 1. Пересекающиеся прямые. 2. Параллельные прямые. 3. Скрещивающиеся прямые.
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.
Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°. а b
Угол между двумя параллельными прямыми равен 0° .
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми и.
Угол между скрещивающимися прямыми, как и между прямыми одной плоскости, не может быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°, называются перпендикулярными. a b a 1 c c 1 d
Угол между скрещивающими прямыми Пусть AB и CD – две скрещивающиеся прямые. Возьмём произвольную точку М 1 пространства и проведём через неё прямые А 1 В 1 и C 1 D 1 , соответственно параллельные прямым AB и CD . А В C D А 1 В 1 C 1 D 1 M 1 φ Если угол между прямыми А 1 В 1 и C 1 D 1 равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ.
Найдём угол между скрещивающимися прямыми AB и CD В качестве точки M 1 можно взять любую точку на одной из скрещивающихся прямых. А В C D M 1 А 1 В 1 φ
Физкультминутка для глаз
Покажите перпендикулярные скрещивающиеся прямые в окружении.
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b . 90° 45° Ответ Ответ
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b . 90° 60° Ответ Ответ
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b 90° 90° Ответ Ответ
Домашнее задание: §4 (стр. 85-89), №268, №269.
Физкультминутка
Задача №1 В правильной пирамиде SABCD , все ребра которой равны 1, точка E – середина ребра SC . Найдите угол между прямыми AD и BE .
Работа в классе: Задачи: № 263 №265 №267
Предварительный просмотр:
УТВЕРЖДАЮ
Учитель математики
Л. Р. Вольняк
«__» ________ 2016г.
Тема : "Угол между прямыми"
Обучающие:
Развивающие:
Воспитательные:
Тип урока: Изучение нового материала.
Методы: словесный (рассказ), наглядный (презентация), диалогический.
- Организационный момент.
- Приветствие.
- Актуализация знаний.
- Каково взаимное расположение двух прямых в пространстве?
- Сколько углов образуется при пересечении двух прямых в пространстве?
- Как определить угол между пересекающимися прямыми?
Слад3
- Основание призмы ABCDA 1 B 1 C 1 D 1 – трапеция. Какие из следующих пар прямых являются скрещивающими?
Ответ: ABи CC 1 ,A 1 D 1 и CC 1 .
- Изучение нового материала.
Слайд 4
Расположение прямых в пространстве и угол между ними.
- Пересекающиеся прямые.
- Параллельные прямые.
- Скрещивающиеся прямые.
Слайд 5
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.
Слайд 6
Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.
Слайд 7
Угол между двумя параллельными прямыми равен 0°.
Слайд 8
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
Слайд 9 a и b и .
Слайд 10
Угол между скрещивающимися прямыми, как и между прямыми одной плоскости, не может быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°, называются перпендикулярными.
Слайд 11
Угол между скрещивающими прямыми.
Пусть ABи CD – две скрещивающиеся прямые.
Возьмём произвольную точку М 1 пространства и проведём через неё прямые А 1 В 1 и C 1 D 1 , соответственно параллельные прямым AB и CD.
Если угол между прямыми А 1 В 1 и C 1 D 1 равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ.
Слайд 12
Найдём угол между скрещивающимися прямыми ABи CD.
В качестве точки M 1 можно взять любую точку на одной из скрещивающихся прямых.
Слайд 13
Физкультминутка
Слайд 14
1. Покажите перпендикулярные скрещивающиеся прямые в окружении.
Слайд 15
2. Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.
 а) 90°;
а) 90°;
 б) 45°;
б) 45°;
Слайд 16
 в) 60°;
в) 60°;
 г) 90°;
г) 90°;
Слайд 17
 д) 90°;
д) 90°;
 е) 90°.
е) 90°.
- Закрепление нового материала
Слайд 19
Физкультминутка
Слайд 20
№1.
В правильной пирамиде SABCD , все ребра которой равны 1, точка E – середина ребра SC .Найдите угол между прямыми AD и BE .
Решение:
Искомый угол = углу CBE .Треугольник SBC-равносторонний.
ВE – биссектриса угла = 60. Угол CBE равен 30.
Ответ :30 °.
№263.
Ответ:
Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a 1 и b 1 , причем a 1 || a, b 1 || b.
№265.
Угол между прямымиaи bравен 90°. Верно ли, что прямые aи bпересекаются?
Ответ:
Неверно, так как прямые могут либо пересекаться, либо скрещиваться.
№267.
DABC – тетраэдр, точка О и F – середины ребра AD и CDсоответственно, отрезок TK – средняя линия треугольника ABC.
- Чему равен угол между прямымиOFи CB?
- Верно ли, что угол между прямымиOFи TK равен 60°?
- Чему равен угол между прямымиTFи DB?
Решение:
Дано: DABC,
О – середина AD,
F – серединаCD,
ТК – средняя линия ∆АВС.
Решение:
- Рефлексия
- Что мы узнали нового?
- Справились ли мы с теми задачами которые были заданы в начале урока?
- Какие задачи мы научились решать?
- Домашнее задание.
§4 (стр. 85-89), №268, №269.
Предварительный просмотр:
УТВЕРЖДАЮ
Учитель математики
Л. Р. Вольняк
«__» ________ 2016г.
Тема : "Угол между прямыми"
Обучающие: с помощью практических заданий обеспечить понимание учащимися определения угла между пересекающимися, параллельными и скрещивающимися прямыми;
Развивающие: развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание; вырабатывать самостоятельность в освоении новых знаний.
Воспитательные: воспитывать у учащихся ответственное отношение к учебному труду, волевые качества; формировать эмоциональную культуру и культуру общения.
Тип урока : обобщение и систематизация знаний и умений.
Методы: словесный (рассказ), диалогический.
- Организационный момент.
- Приветствие.
- Сообщение целей и задач урока.
- Мотивация изучения нового материала.
- Психолого-педагогическая настройка учащихся на предстоящую деятельность.
- Проверка присутствующих на уроке;
- Проверка домашнего задания
№268
ABCDA 1 B 1 C 1 D 1 – прямоугольный параллелепипед, точка О и Т – середины рёбер СС 1 и DD 1 соответственно. а) Верно ли, что угол между прямыми AD и TO равен 90°? б)Чему равен угол между прямыми A 1 B 1 и BC?
Решение:
а) Верно, так как TO || DC => (AD, TO) = ADC = 90° (ABCD – прямоугольник).
б)BC || B 1 C 1 => (A 1 B 1 , BC) = A 1 B 1 C 1 = 90°.
Ответ: 90°, 90°.
№269
ABCDA 1 B 1 C 1 D 1 – куб. а) Верно ли, что угол между прямыми A 1 B и C 1 D равен 90°? б) Найдите угол между прямыми В 1 О и C 1 D. в) Верно ли, что угол между прямыми АС и C 1 D равен 45°?
Решение:
а) Верно, так как В 1 А || C 1 D => (A 1 B, C 1 D)= (B 1 A, A 1 B) = 90°, как угол между диагоналями квадрата.
б) 1. В 1 А || C 1 D=> (B 1 O, C 1 D) = AB 1 O.
2. в Δ AB 1 С AB 1 = В 1 С = АС как диагонали равных квадратов В 1 О – медиана и биссектриса AB 1 С=60° => AB 1 O=30°.
в) нет, так как C 1 D || BA => (AС, C 1 D)= B 1 АC=60° как угол равностороннего Δ AB 1 С.
Ответ: б) 30°.
- Актуализация знаний.
Метод: фронтальный опрос (устно) :
- Какие разделы изучает геометрия?
- Чему равен угол между параллельными прямыми?
- Какие фигуры изучает планиметрия, а какие стереометрия?
- Какой угол называется скрещивающимся?
- Как называются две прямые скрещивающиеся, которые образуют угол 90°?
- Закрепление изученного.
Диктант (10 мин):
Вариант 1:
Ребро куба равно а .
Найти : (АВ 1 ,СС 1 )
Решение:
СС1‖ВВ1
(АВ1,СС1)= АВ1В
АВ1В=45˚
Ответ: (АВ1,СС1)=45˚
- Пусть а и b – скрещивающиеся прямые, а прямая b 1 || b. Верное ли утверждение, что угол между прямыми а и b равен углу между прямыми a и b 1 ? Если да, то почему?
Вариант 2:
- Какой угол называется углом между скрещивающими прямыми?
Ребро куба равно а .
перпендикулярности двух прямых.
1. Если прямые L 1 и L 2 заданы общими уравнениями
А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0,
то угол между ними равен углу между их нормалями, то есть между векторами {A 1 ,B 1 } и {A 2 ,B 2 }. Следовательно,
Условия параллельности и перпендикулярности прямых тоже сводятся к условиям параллельности и перпендикулярности нормалей:
Условие параллельности, (7.11)
![]() - условие перпендикулярности. (7.12).
- условие перпендикулярности. (7.12).
2. Если прямые заданы каноническими уравнениями (7.5), по аналогии с пунктом 1 получим:
 , (7.13)
, (7.13)
Условие параллельности, (7.14)
![]() - условие перпендикулярности. (7.16).
- условие перпендикулярности. (7.16).
Здесь и - направляющие векторы прямых.
3. Пусть прямые L 1 и L 2 заданы уравнениями с угловыми коэффициентами (7.8)
у = k 1 x +b 1 и y = k 2 x + b 2 , где ![]() , а α 1 и α 2 – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α 2 - α 1 . Тогда
, а α 1 и α 2 – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α 2 - α 1 . Тогда
Условие параллельности имеет вид: k 1 =k 2 , (7.18)
условие перпендикулярности – k 2 =-1/k 1 , (7.19)
поскольку при этом tgφ не существует.
Расстояние от точки до прямой.
Рассмотрим прямую L и проведем перпендикуляр ОР к ней из начала координат (предполагаем, что прямая не проходит через начало координат). Пусть n – единичный вектор, направление которого совпадает с ОР. Составим уравнение прямой L, в которое входят два параметра: р – длина отрезка ОР и α – угол между ОР и Ох.
Для точки М, лежащей на L, проекция вектора ОМ на прямую
ОР равна р. С другой стороны, пр n OM=n·OM. Поскольку
n ={cosα , sinα }, a OM ={x,y }, получаем, что
x cosα + y sinα = p, или
x cosα + y sinα - p = 0 - (7.20)
Искомое уравнение прямой L , называемое нормальным
уравнением прямой (термин «нормальное уравнение» связан
с тем, что отрезок ОР является перпендикуляром, или нормалью, к данной прямой).
Определение 7.2. Если d – расстояние от точки А до прямой L , то отклонение δ точки А от прямой L есть число +d , если точка А и начало координат лежат по разные стороны от прямой L , и число –d , если они лежат по одну сторону от L .
Теорема 7.1. Отклонение точки А(х 0 ,у 0 ) от прямой L , заданной уравнением (7.20), определяется по формуле:
Доказательство.
Проекция OQ вектора ОА на направление ОР равна
n·OA =x 0 cosα + y 0 sinα. Отсюда δ = PQ=OQ-OP=OQ-p =
x 0 cosα + y 0 sinα - p , что и требовалось доказать
Следствие.
Расстояние от точки до прямой определяется так:
Замечание. Для того, чтобы привести общее уравнение прямой к нормальному виду, нужно умножить его на число , причем знак выбирается противоположным знаку свободного члена С в общем уравнении прямой. Это число называется нормирующим множителем.
Пример. Найдем расстояние от точки А (7,-3) до прямой, заданной уравнением
3х + 4у + 15 = 0. А ² + B ²=9+16=25, C =15>0, поэтому нормирующий множитель равен
1/5, и нормальное уравнение прямой имеет вид: ![]() Подставив в его левую часть вместо х и у координаты точки А,
получим, что ее отклонение от прямой равно
Подставив в его левую часть вместо х и у координаты точки А,
получим, что ее отклонение от прямой равно
![]() Следовательно, расстояние от точки А
до данной прямой равно 4,8.
Следовательно, расстояние от точки А
до данной прямой равно 4,8.
8. Прямая и плоскость в пространстве. Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью.
Отметим, что многие утверждения и формулы, касающиеся плоскости в пространстве, доказываются и выводятся так же, как при изучении прямой на плоскости, поэтому в этих случаях будут даваться ссылки на предыдущую лекцию.
Плоскость в пространстве.
Получим сначала уравнение плоскости, проходящей через точку М 0 (х 0 ,у 0 ,z 0 ) перпендикулярно вектору n = {A,B,C },называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z ) вектор М 0 М = {x - x 0 , y - y 0 , z - z 0 ) ортогонален вектору n , следовательно, их скалярное произведение равно нулю:
A(x - x 0 ) + B(y - y 0 ) + C(z - z 0 ) = 0. (8.1)
Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
После приведения подобных можно записать уравнение (8.1) в виде.